人教版七年级数学上册单元测试 第四章达标测试卷（含答案）

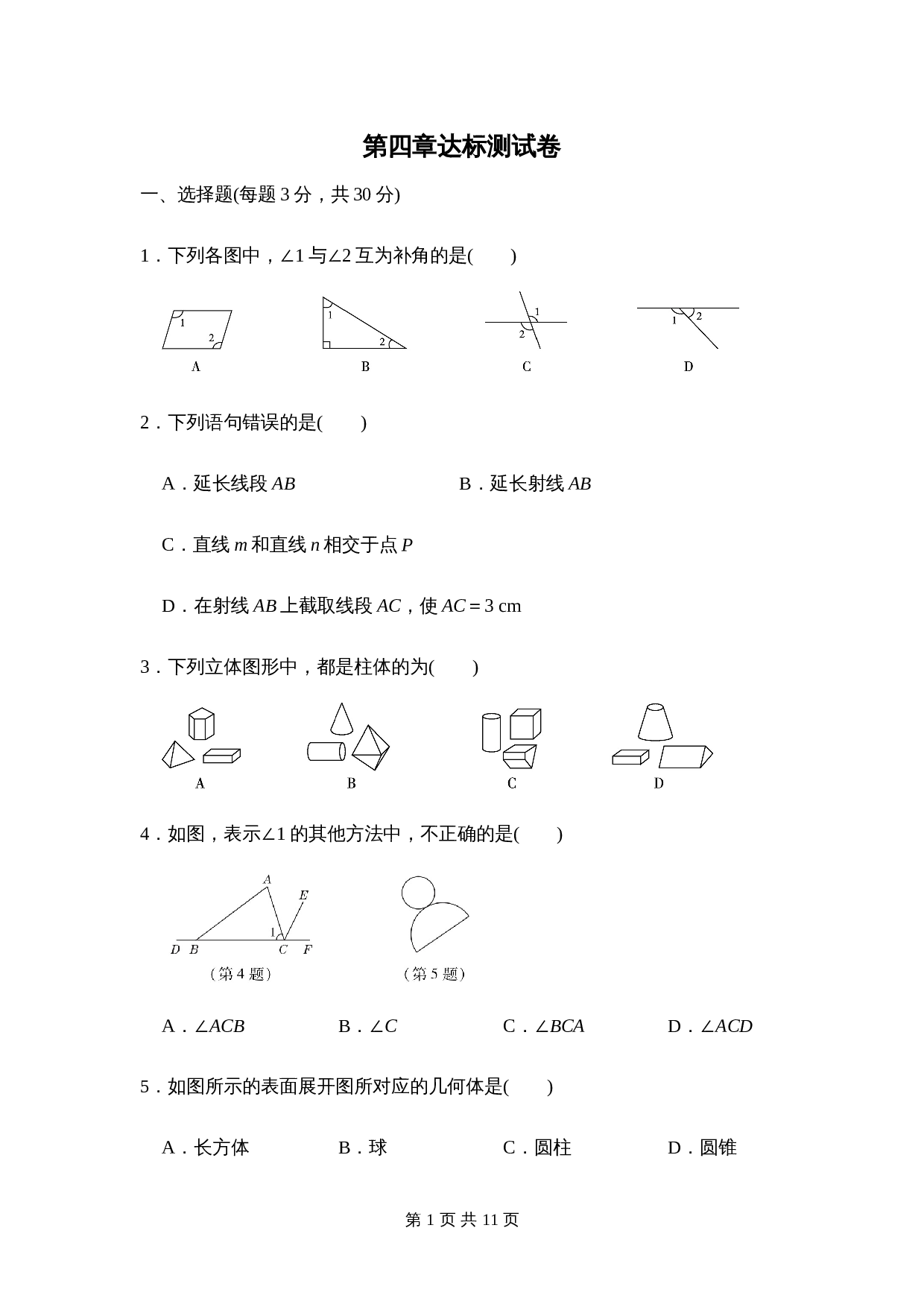
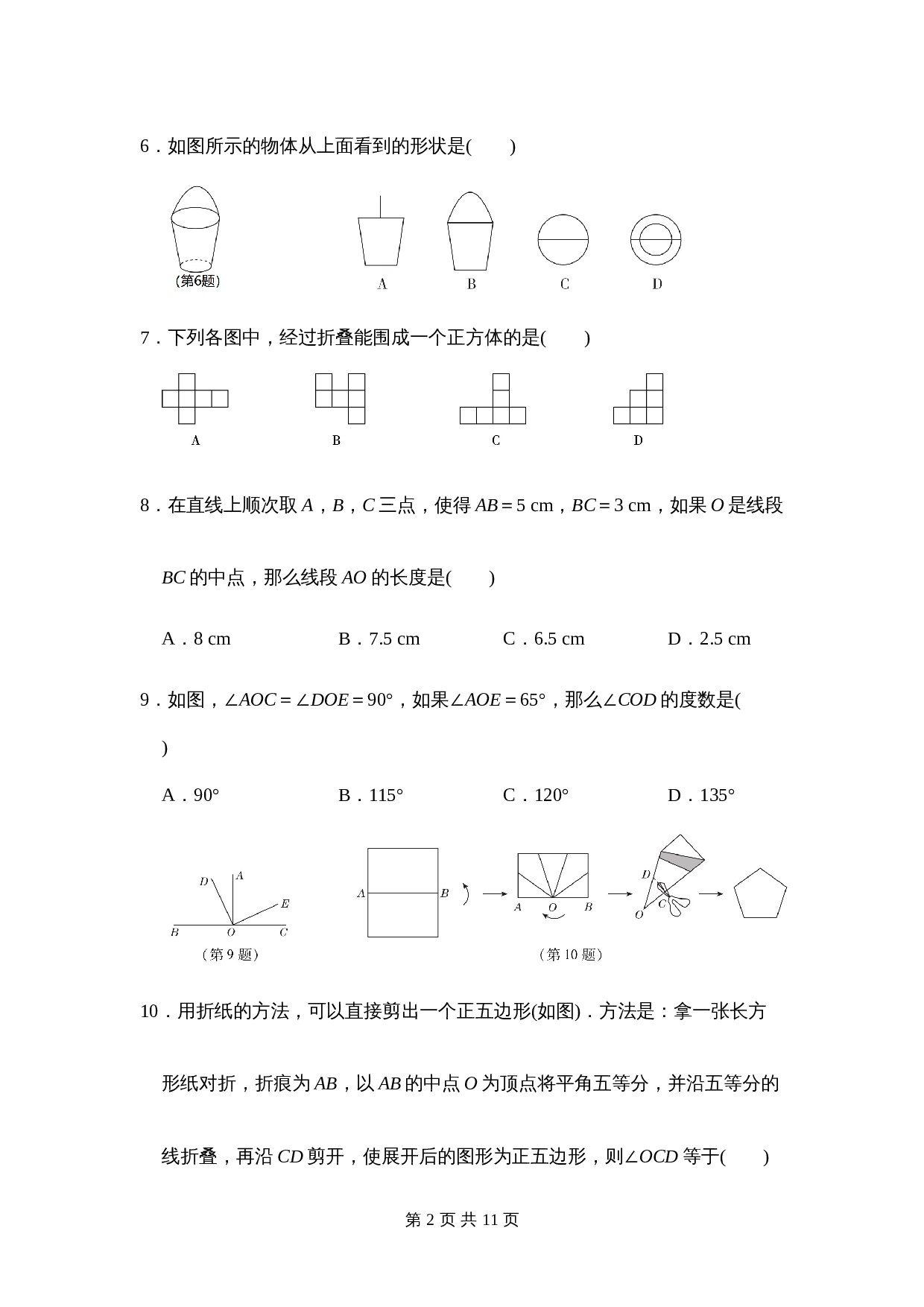
第四章达标测试卷 一、选择题 ( 每题 3 分，共 30 分 ) 1 ．下列各图中， ∠1 与 ∠2 互为补角的是 ( 　　 ) 2 ．下列语句错误的是 ( 　　 ) A ．延长线段 AB B ．延长射线 AB C ．直线 m 和直线 n 相交于点 P D ．在射线 AB 上截取线段 AC ，使 AC ＝ 3 cm 3 ．下列立体图形中，都是柱体的为 ( 　　 ) 4 ．如图，表示 ∠1 的其他方法中，不正确的是 ( 　　 ) A ． ∠ ACB B ． ∠ C C ． ∠ BCA D ． ∠ ACD 5 ．如图所示的表面展开图所对应的几何体是 ( 　　 ) A ．长方体 B ．球 C ．圆柱 D ．圆锥 6 ．如图所示的物体从上面看到的形状是 ( 　　 ) 7 ．下列各图中，经过折叠能围成一个正方体的是 ( 　　 ) 8 ．在直线上顺次取 A ， B ， C 三点，使得 AB ＝ 5 cm ， BC ＝ 3 cm ，如果 O 是线段 BC 的中点，那么线段 AO 的长度是 ( 　　 ) A ． 8 cm B ． 7.5 cm C ． 6.5 cm D ． 2.5 cm 9 ．如图， ∠ AOC ＝ ∠ DOE ＝ 90° ，如果 ∠ AOE ＝ 65° ，那么 ∠ COD 的度数是 ( 　　 ) A ． 90° B ． 115° C ． 120° D ． 135° 10 ．用折纸的方法，可以直接剪出一个正五边形 ( 如图 ) ．方法是：拿一张长方形纸对折，折痕为 AB ，以 AB 的中点 O 为顶点将平角五等分，并沿五等分的线折叠，再沿 CD 剪开，使展开后的图形为正五边形，则 ∠ OCD 等于 ( 　　 ) A ． 108° B ． 90° C ． 72° D ． 60° 二、填空题 ( 每题 3 分，共 24 分 ) 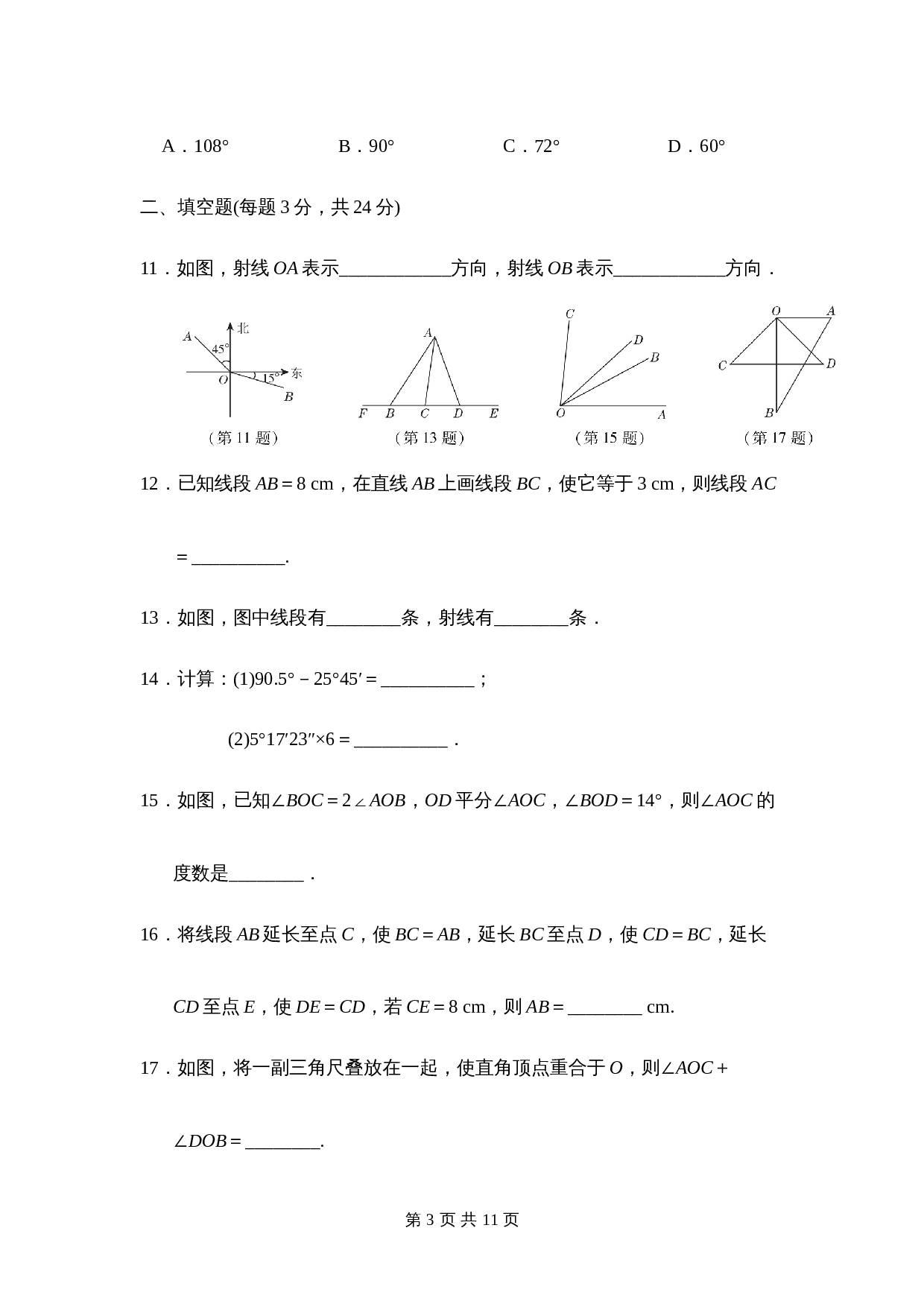11 ．如图，射线 OA 表示 ____________ 方向，射线 OB 表示 ____________ 方向． 12 ．已知线段 AB ＝ 8 cm ，在直线 AB 上画线段 BC ，使它等于 3 cm ，则线段 AC ＝ __________. 13 ．如图，图中线段有 ________ 条，射线有 ________ 条． 14 ．计算： (1)90.5° － 25°45′ ＝ __________ ； (2)5°17′23″×6 ＝ __________ ． 15 ．如图，已知 ∠ BOC ＝ 2∠ AOB ， OD 平分 ∠ AOC ， ∠ BOD ＝ 14° ，则 ∠ AOC 的度数是 ________ ． 16 ．将线段 AB 延长至点 C ，使 BC ＝ AB ，延长 BC 至点 D ，使 CD ＝ BC ，延长 CD 至点 E ，使 DE ＝ CD ，若 CE ＝ 8 cm ，则 AB ＝ ________ cm. 17 ．如图，将一副三角尺叠放在一起，使直角顶点重合于 O ，则 ∠ AOC ＋ ∠ DOB ＝ ________. 18 ．如图是由一些小立方块所搭立体图形分别从正面、左面、上面看到的图形，若在所搭立体图形的基础上 ( 不改变原立体图形中小立方块的位置 ) ，继续添加相同的小立方块，以搭成一个大正方体，至少还需要 ________ 个 小立 方块． 三、解答题 (19 ， 21 题每题 6 分， 20 ， 22 ， 24 题每题 10 分，其余每题 12 分，共 66 分 ) 19 ．如图， A ， B 两个村庄在河 m 的两侧，连接 AB ，与 m 交于点 C ，点 D 在 m 上，连接 AD ， BD ，且 AD ＝ BD . 若要在河上建一座桥，使 A ， B 两村来往最便捷，则应该把桥建在点 C 还是点 D ？请说明理由． 20 ．如图，已知线段 a ， b ，画一条线段，使它等于 3 a － b ( 不要求写画法 ) ． 21 ．如图所示的立体图形是由七块积木搭成的，这几块积木是大小相同的正方体，请画出这个立体图形分别从正面、左面、上面看到的图形． 22 ．如图，点 C 是 AB 的中点 ， D ， E 分别是线段 AC ， CB 上的点，且 AD ＝ AC ， DE ＝ AB ，若 AB ＝ 24 cm ，求线段 CE 的长． 23 ．如图， OD 平分 ∠ BOC ， OE 平分 ∠ AOC ， ∠ BOC ＝ 60° ， ∠ AOC ＝ 58°. (1) 求出 ∠ AOB 及其补角的度数； (2)① 请求出 ∠ DOC 和 ∠ AOE 的度数； ② 判断 ∠ DOE 与 ∠ AOB 是否互补，并说明理由． 24 ．如图，把一根绳子对折成线段 AB ，从点 P 处把绳子剪断，已知 AP  BP ＝ 23 ，若剪断后的各段绳子中最长的一段为 60 cm ，求绳子的原长． 25 ．已知 O 为直线 AB 上一点， ∠ COE 是 直角， OF 平分 ∠ AOE . (1) 如图 ① ，若 ∠ COF ＝ 34° ，则 ∠ BOE ＝ ________ ；若 ∠ COF ＝ n ° ，则 ∠ BOE ＝ ________ ； ∠ BOE 与 ∠ COF 的数量关系为 ________________ ． (2) 当射线 OE 绕点 O 逆时针旋转到如图 ② 的位置时， (1) 中 ∠ BOE 与 ∠ COF 的数量关系是否仍然成立？请说明理由． (3) 在图 ③ 中，若 ∠ COF ＝ 65° ，在 ∠ BOE 的内部是否存在一条射线 OD ，使得 2∠ BOD 与 ∠ AOF 的和等于 ∠ BOE 与 ∠ BOD 的差的一半？若存在，请求出 ∠ BOD 的度数；若不存在，请说明理由． 答案 一、 1. D 　 2. B 　 3. C 　 4. B 　 5. D 　 6. D 7 ． A 　 8. C 　 9. B 　 10. B 二、 11. 北偏西 45°( 西北 ) ；南偏东 75° 12 ． 11 cm 或 5 cm 　 13. 6 ； 6 14 ． (1)64°45′ 　 (2)31°44′18″ 15 ． 84° 　 16. 54 　 17. 180° 　 18. 54 三、 19. 解：应该把桥建在点 C . 理由：两点之间，线段最短 ． 20 ． 解：如图， AE ＝ 3 a － b . 21 ． 解：如图所示 ． 22 ． 解：因为点 C 是 AB 的中点， 所以 AC ＝ BC ＝ AB ＝ ×24 ＝ 12(cm) ． 所以 AD ＝ AC ＝ ×12 ＝ 8(cm) ． 所以 CD ＝ AC － AD ＝ 12 － 8 ＝ 4(cm) ． 因为 DE ＝ AB ＝ ×24 ＝ 14.4(cm) ， 所以 CE ＝ DE － CD ＝ 14.4 － 4