苏科版七年级数学下册试题试卷 期中测试卷02（含解析）

期中测试卷0 2 满分100分 时间120分钟 一、选择题（共10小题，每小题2分，共20分） 1． 的值是(       )． A． B． C． D． 2．当 x ＝﹣3时，多项式 ax 5 + bx 3 + cx ﹣5的值是7，那么当 x ＝3时，它的值是（       ） A．﹣3 B．﹣7 C．7 D．﹣17 3．下列结论：①如果 ，那么 ；②在∆ ABC 中，若 ，则∆ ABC 为直角三角形；③ ；④一个多边形的边数每增加一条，这个多边形的内角和就增加 ；⑤任意一个三角形三条高所在的直线相交于一点，且这点一定在三角形的内部．其中错误结论有（       ） A．2个 B．3个 C．4个 D．5个 4．下列说法错误的是（     ） A．等角的余角相等 B．同位角相等两直线平行 C．两条平行线间的距离处处相等 D．相等的角是对顶角 5．如图，已知 AB ∥ CD ， AF 交 CD 于点 E ，且 BE ⊥ AF ，∠ BED ＝50°，则∠ A 的度数是（　　） A．40° B．50° C．80° D．90° 6．下列四个图形中，不能通过基本图形平移得到的是（       ） A． B． C． D． 7．如图，四边形 ABCD 是梯形， ， 与 的角平分线交于点 E ， 与 的角平分线交于点 F ，则 与 的大小关系为（     ） A． B． C． D．无法确定 8．对式子 进行去括号运算，结果正确的是（ ） A． B． C． D． 9．下列等式成立的是（　　） A．（ n ﹣ m ）（﹣ m ﹣ n ）＝ m 2 ﹣ n 2 B．（ n ﹣ m ） 2 ＝ n 2 ﹣ m 2 C．（ a ﹣4）（ a +4）＝ a 2 ﹣4 D．（2 x ﹣3 y ）（2 x +3 y ）＝2 x 2 ﹣3 y 2 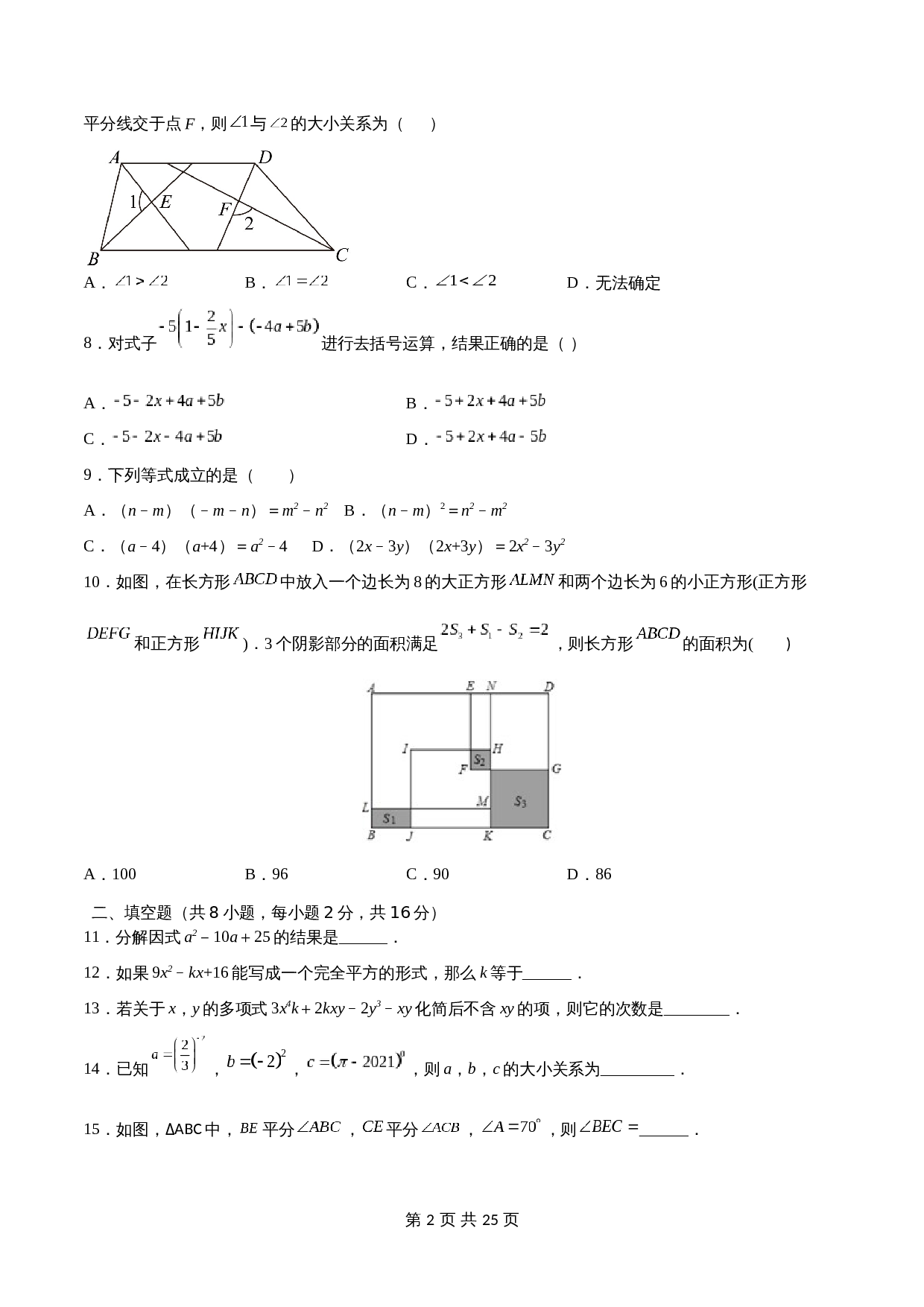10．如图，在长方形 中放入一个边长为8的大正方形 和两个边长为6的小正方形(正方形 和正方形 )．3个阴影部分的面积满足 ，则长方形 的面积为(　　 ) A．100 B．96 C．90 D．86 二、填空题（共8小题，每小题2分，共16分） 11．分解因式 a 2 －10 a ＋25的结果是______． 12．如果9 x 2 ﹣ kx +16能写成一个完全平方的形式，那么 k 等于______． 13．若关于 x ， y 的多项式3 x 4 k ＋2 kxy ﹣2 y 3 ﹣ xy 化简后不含 xy 的项，则它的次数是________． 14．已知 ， ， ，则 a ， b ， c 的大小关系为_________． 15．如图，∆ ABC 中， 平分 ， 平分 ， ，则 ______． 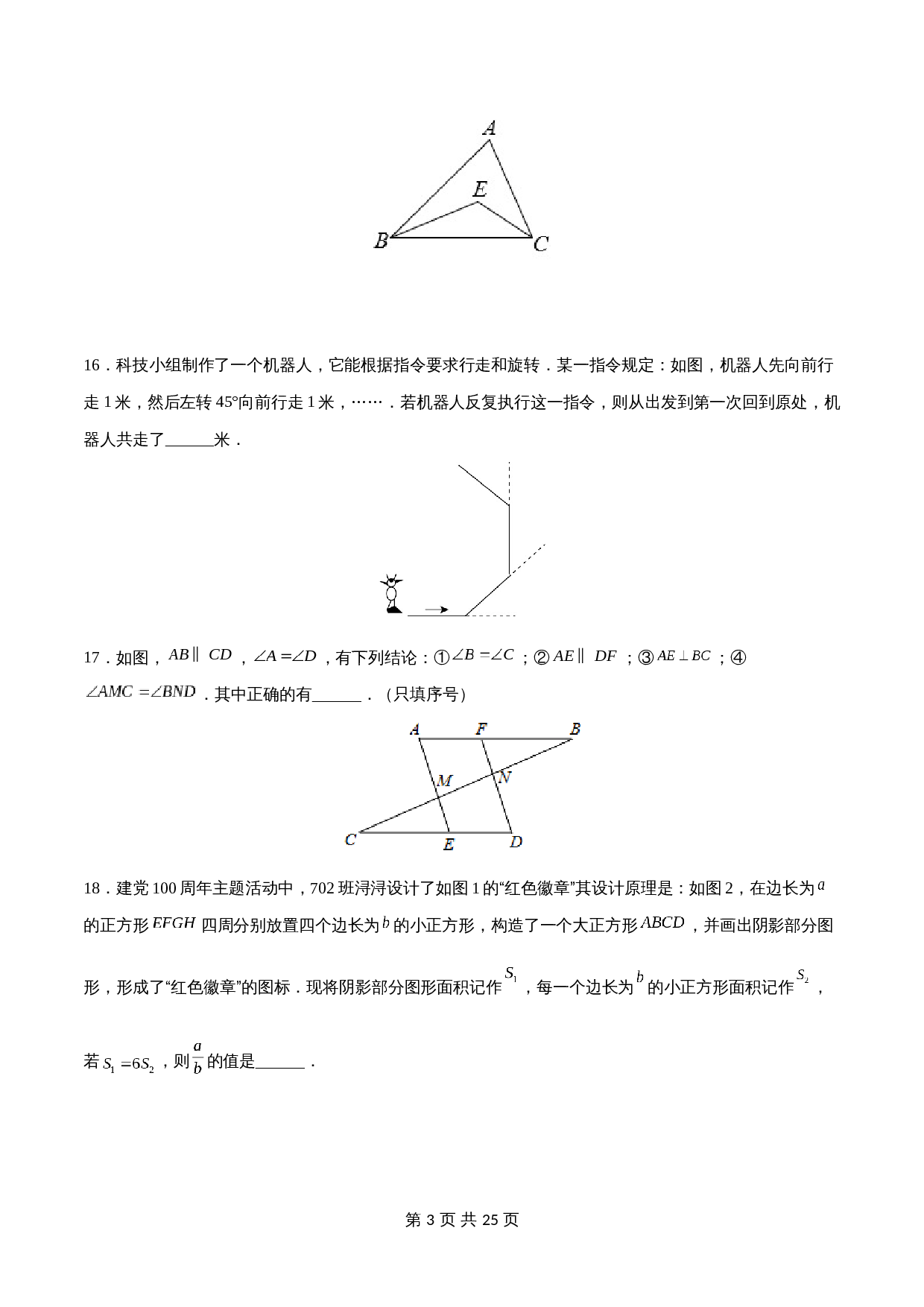16．科技小组制作了一个机器人，它能根据指令要求行走和旋转．某一指令规定：如图，机器人先向前行走1米，然后左转45°向前行走1米，……．若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了______米． 17．如图， ， ，有下列结论：① ；② ；③ ；④ ．其中正确的有______．（只填序号） 18．建党100周年主题活动中，702班浔浔设计了如图1的“红色徽章”其设计原理是：如图2，在边长为 的正方形 四周分别放置四个边长为 的小正方形，构造了一个大正方形 ，并画出阴影部分图形，形成了“红色徽章”的图标．现将阴影部分图形面积记作 ，每一个边长为 的小正方形面积记作 ，若 ，则 的值是______． 三、解答题（共64分） 19.（5分） 计算：（﹣3 a 2 ） 3 +（4 a 3 ） 2 ﹣ a 2 • a 4 ． 20.（5分） 化简： 21.（5分） 先化简，再求值：（ a +2 b ﹣1）（ a ﹣2 b +1）﹣4 b （ a ﹣ b +1），其中 a ， b ． 22.（6分） 如图，在 的正方形网格中，线段 的两个端点 ， 在格点上，根据要求画出端点都在格点上的一条线段． (1)在图1中画出与 相等的线段 ； (2)在图2中画出与 平行的最长线段 ． 23.（6分） 如图，已知 ， D 为△ ABC 的边 BC 上的一点，且 ， ．求∠ B 的度数． 24.（6分） 探究多边形内角和时，我们常把多边形转化成三角形，再根据三角形内角和为180°得出多边形内角和．如图是探究多边形内角和一种方法，请根据图示，完成填空 （1）四边形内角和：4×180°﹣360°＝4×180°﹣2×180°＝2×180° ； （2）五边形内角和：5×180°﹣360°＝5×180°﹣2×180°＝ 　 　 ； （3）六边形内角和：6×180°﹣360°＝6×180°﹣2×180°＝ 　 　 ； … （4） n 边形内角和： 　 　 ＝ 　 　 ＝ 　 　 ． 25.（6分） 从边长为 a 的正方形中剪掉一个边长为 b 的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）． (1)上述操作能验证的等式是______．（请选择正确的选项） A ． a 2 ﹣ b 2 ＝（ a + b ）（ a ﹣ b ） B ． a 2 ﹣2 ab + b 2 ＝（ a ﹣ b ） 2 C ． a 2 + ab ＝ a （ a + b ） (2)若 x 2 ﹣ y 2 ＝16， x + y ＝8，求 x ﹣ y 的值 ； (3)用简便计算： ． 26.（6分） 如图，点 D 在 AC 上，点 F ， G 分别在 AC ， BC 的延长线上， CE 平分 并分别交 BD ， AB 于点 H 和 E ，且 ． (1)若 ，求 的度数 ； (2)若 ，求证： ． 27.（9分） 如图1，在△ ABC 中，∠ B ＝65°，∠ BAC ＝75°， D 为 AC 边上一点，分别过点 A 、 D 作 BC 、 AB 的平行线交于点 E ． （1）求∠ E 的度数． （2）点 P 为直线 AC 上的一个动点，过点 P 作 PF ∥ AE ，且 PF ＝ AE ，连 DF ． ①如图2，当点 P 在点 C 的右侧，且∠ PFD ＝25°时，判断 DE 与 DF 的位置关系，并说明理由． ②在整个运动中，是否存在点 P ，使得∠ PFD ＝2∠ EDF ？若存在，请求出∠ PFD 的度数，若