专题18 平行四边形
1. 平行四边形:两组对边分别平行的四边形
.
2. 平行四边形的性质
(1)平行四边形的
平行;
(2)平行四边形的
相等;
(3)平行四边形的
相等;
(4)平行四边形的对角线互相
.
3
.
平行四边形的判定
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别
的四边形是平行四边形;
(3)两组对角分别
的
四边形是平行四边形;
(4)对角线互相
的四边形是平行四边形;
(5)一组对边
的四边形是平行四边形
【考点1】
平行四边形的性质
【例1】
(2022·四川内江)如图,在▱
ABCD
中,已知
AB
=12,
AD
=8,∠
ABC
的平分线
BM
交
CD
边于点
M
,则
DM
的长为( )
A.2
B.4
C.6
D.8
【例2】
(2022·黑龙江大庆)如图,将平行四边形
沿对角线
折叠,使点
A
落在
E
处.若
,
,则
的度数为(
)
A.
B.
C.
D.
在解答平行四边形的题型中,往往涉及到三角形的全等证明,在对学生的综合考查方面有一定要求
1.(2022·广东)如图,在
中,一定正确的是( )
A.
B.
C.
D.
2.(2022·江苏无锡)如图,在
ABCD
中,
,
,点
E
在
AD
上,
,则
的值是( )
A.
B.
C.
D.
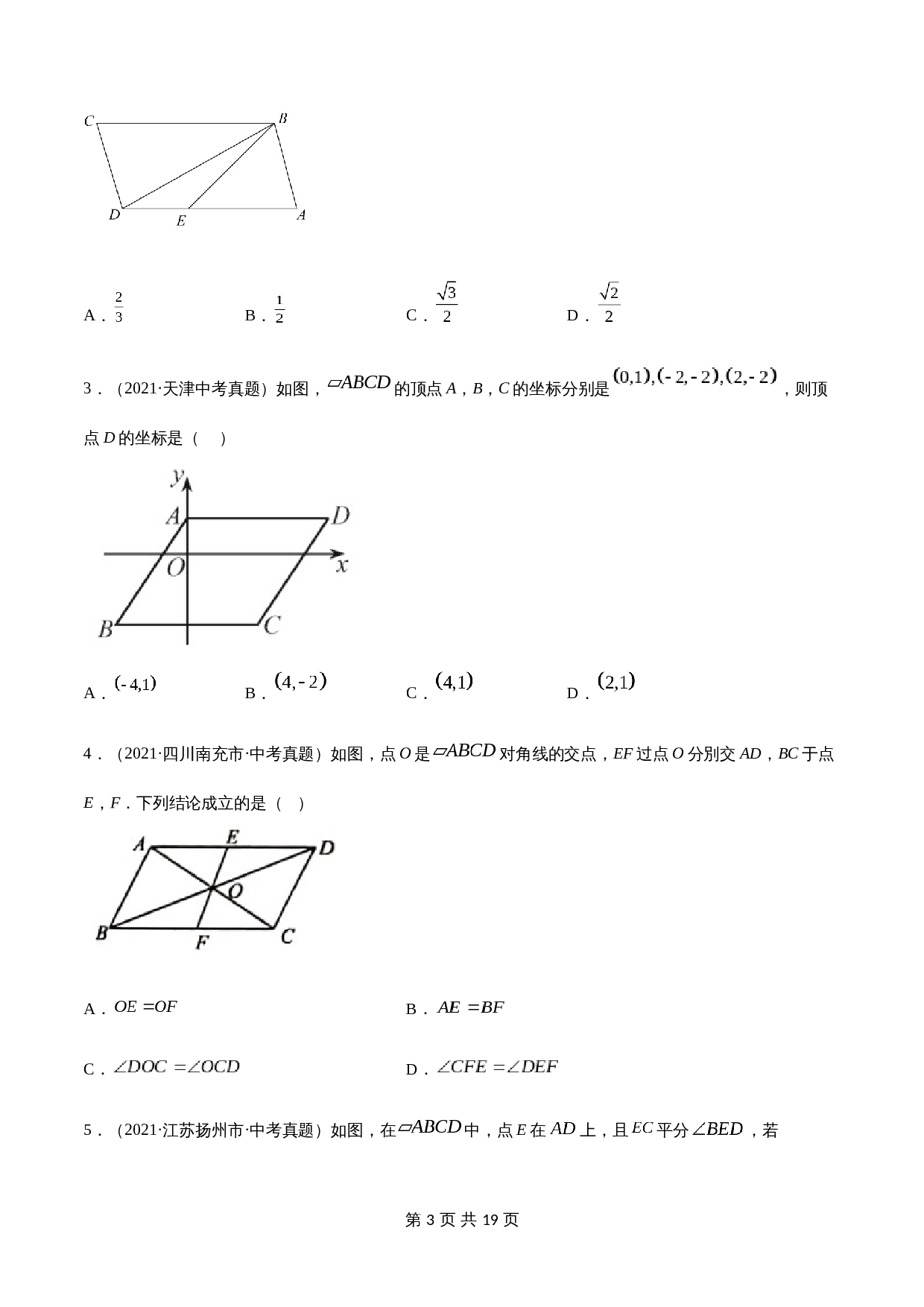
3.(2021·天津中考真题)如图,
的顶点
A
,
B
,
C
的坐标分别是
,则顶点
D
的坐标是( )
A.
B.
C.
D.
4.(2021·四川南充市·中考真题)如图,点
O
是
对角线的交点,
EF
过点
O
分別交
AD
,
BC
于点
E
,
F
.下列结论成立的是( )
A.
B.
C.
D.
5.(2021·江苏扬州市·中考真题)如图,在
中,点
E
在
上,且
平分
,若
,
,则
的面积为________.
【考点2】
平行四边形的判定
【例3】
如图,在下列给出的条件中,能判定四边形
ABCD
为平行四边形的是( )
A.
,
B.
C.
D.
【例4】
(2022·黑龙江大庆)如图,在四边形
中,点
E
,
C
为对角线
上的两点,
.连接
.
(1)求证:四边形
是平行四边形;
(2)若
,求证:
.
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4)对角线互相平分的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形.
1.(2021·四川资阳市)下列命题正确的是(
专题18 平行四边形【考点精讲】(含解析)-2024年中考数学总复习(全国通用)