模型介绍
模型介绍
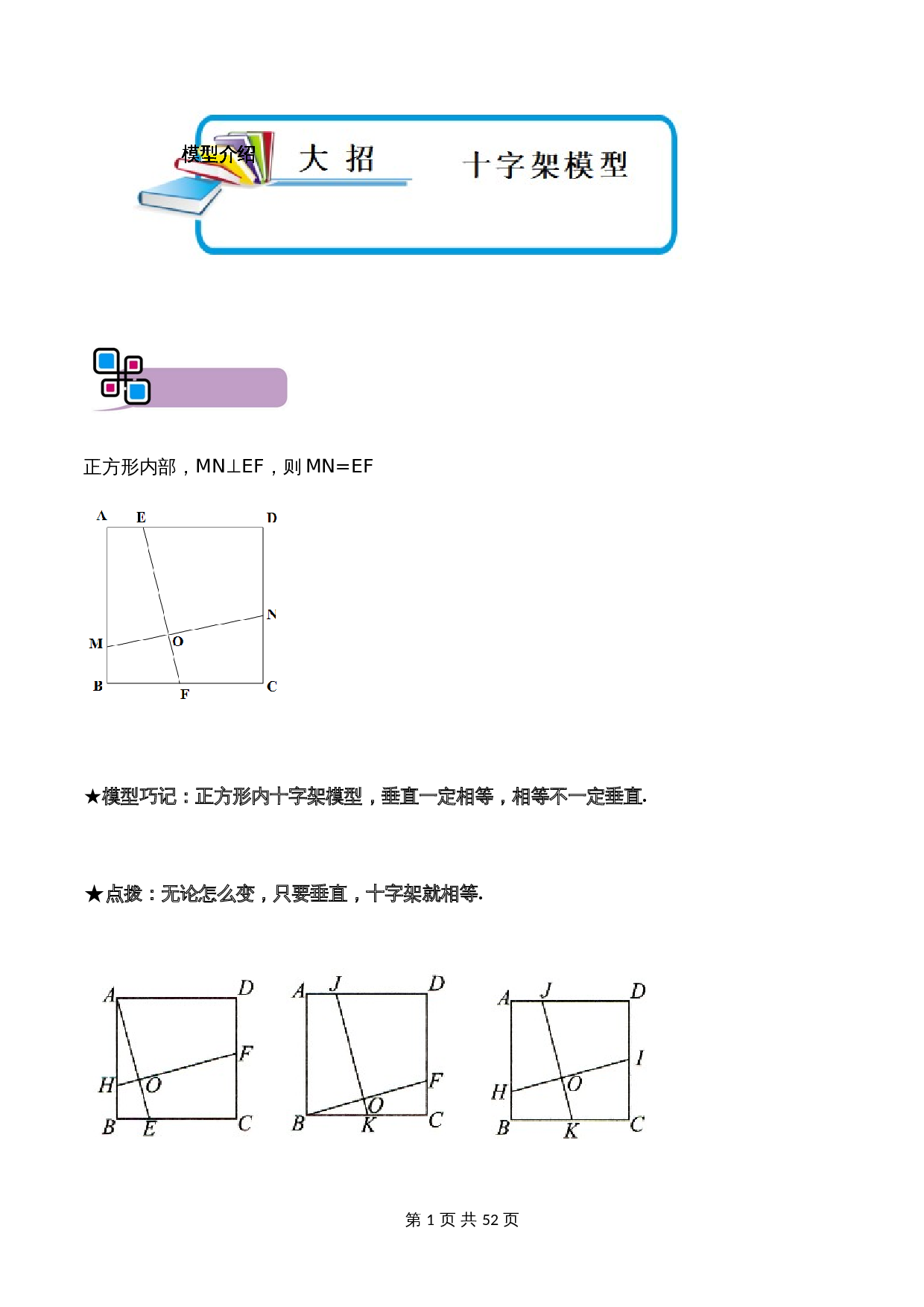
正方形内部,MN⊥EF,则MN=EF
★
模型巧记:
正方形内十字架模型,垂直一定相等,相等不一定垂直.
★
点拨:
无论怎么变,只要垂直,十字架就相等.
例题
精讲
例题
精讲
考点
一、正方形中的十字模型
【
例1
】
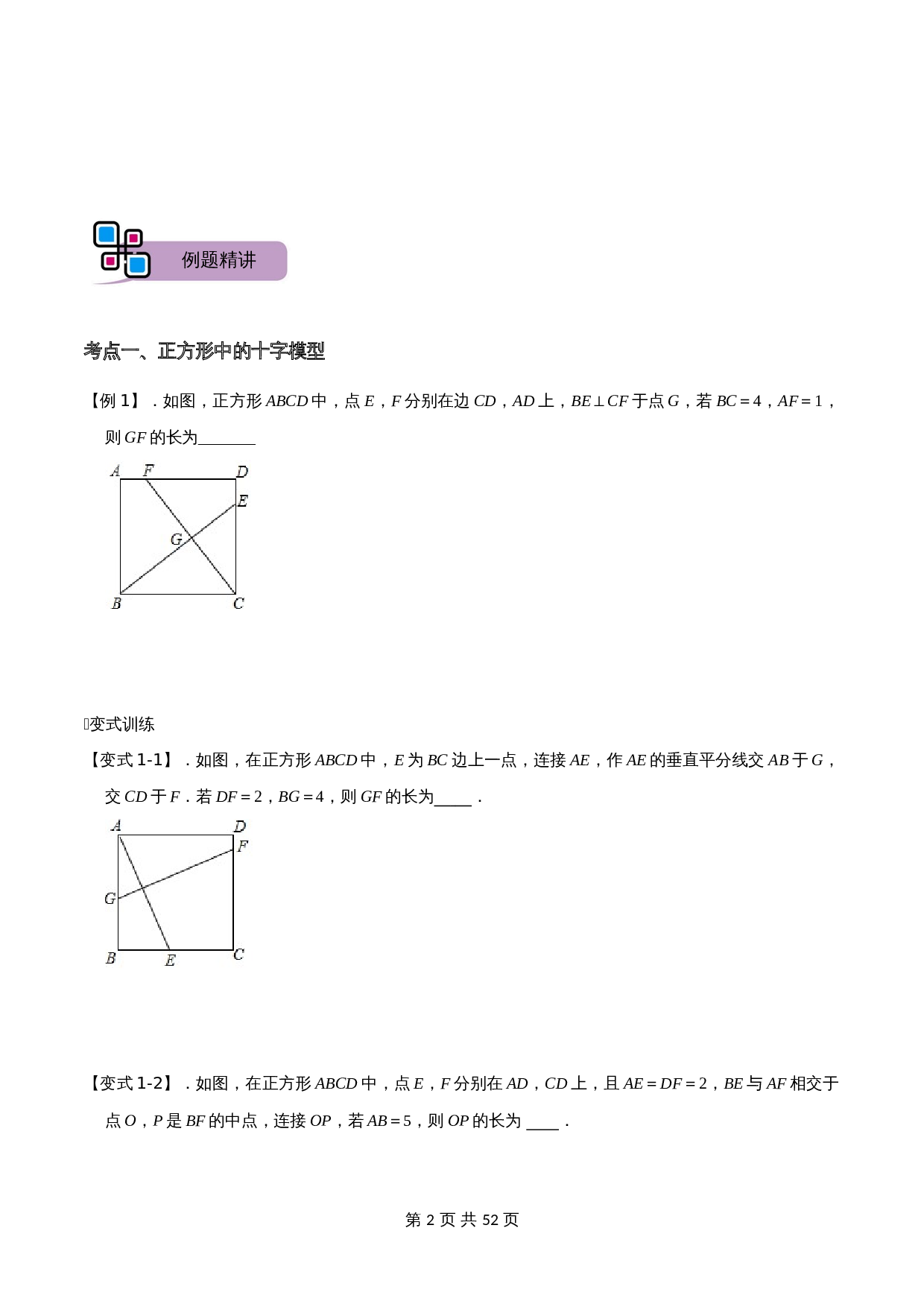
.如图,正方形
ABCD
中,点
E
,
F
分别在边
CD
,
AD
上,
BE
⊥
CF
于点
G
,若
BC
=4,
AF
=1,则
GF
的长为
_______
变式
训练
【
变式1-1
】
.如图,在正方形
ABCD
中,
E
为
BC
边上一点,连接
AE
,作
AE
的垂直平分线交
AB
于
G
,交
CD
于
F
.若
DF
=2,
BG
=4,则
GF
的长为
.
【
变式1-2
】
.如图,在正方形
ABCD
中,点
E
,
F
分别在
AD
,
CD
上,且
AE
=
DF
=2,
BE
与
AF
相交于点
O
,
P
是
BF
的中点,连接
OP
,若
AB
=5,则
OP
的长为
.
【
变式1-3
】
.如图,在正方形
ABCD
中,点
E
是边
BC
上的一点,点
F
在边
CD
的延长线上,且
BE
=
DF
,连接
EF
交边
AD
于点
G
.过点
A
作
AN
⊥
EF
,垂足为点
M
,交边
CD
于点
N
.若
BE
=5,
CN
=8,则线段
AN
的长为
.
考点二:矩形中的十字模型
【
例2
】
.如图,在矩形
ABCD
中,点
E
是边
AB
上一点,将△
BCE
沿
CE
折叠,使点
B
落在
AD
边上的点
F
处,连接
BF
.已知
AD
=5,
AB
=3,求折痕
CE
的长.
变式
训练
【
变式2-1
】
.
如图,把边长为
,
的矩形
对折,使点
和
重合,求折痕
的长.
【
变式2-2
】
.如图,矩形
ABCD
中,
BC
:
AB
=1:2,
F
、
G
分别为
AB
、
DC
边上的动点,连接
GF
,沿
GF
将四边形
AFGD
翻折至四边形
EFGP
,点
E
落在
BC
上,
EP
交
CD
于点
H
,连接
AE
交
GF
于点
O
,连接
CP
,若tan∠
CGP
=
,
GF
=2
,
CP
的长为
.
【
变式2-3
】
.
如图,在矩形
ABCD
中,
AB
=5,
AD
=10.若点
E
是边
AD
上的一个动点,过点
E
作
EF
⊥
AC
且分别交对角线
AC
、直线
BC
于点
O
、
F
,则在点
E
移动的过程中,
AF
+
FE
+
EC
的最小值为
.
实战演练
实战演练
1.如图,在边长为4的正方形
ABCD
中,点
E
、
F
分别是边
BC
、
CD
上的动点,且
BE
=
CF
,连接
BF
、
DE
,则
BF
+
DE
的最小值为( )
A.8
B.4
C.4
D.4
2
.如图,在正方形
ABCD
中,
E
,
F
分别是
AB
,
BC
的中点,
CE
,
DF
交于点
G
,连接
AG
.下列结论:
①
CE
=
DF
;
②
CE
⊥
DF
;
③
∠
AGE
=∠
CDF
.其中正确的结论是(
【解题大招】模型15 十字架模型(含解析)-2024年中考数学复习(全国通用)