考点
2
1
平行四边形
平行四边形的性质与判定是初中数学中四边形知识的开端和基础,正是在平行四边形的基础之上才能逐渐延伸特殊平行四边形的知识和规律。中考数学中,对平行四边形的单独考察难度一般不大,但题型较为广泛,选择、填空、解答题都有可能;但是,该考点的学习隐含了比较多的思想方法,需要学生在整体复习该考点的过程中注重反证法、转化、类比归纳等思想方法的提升。
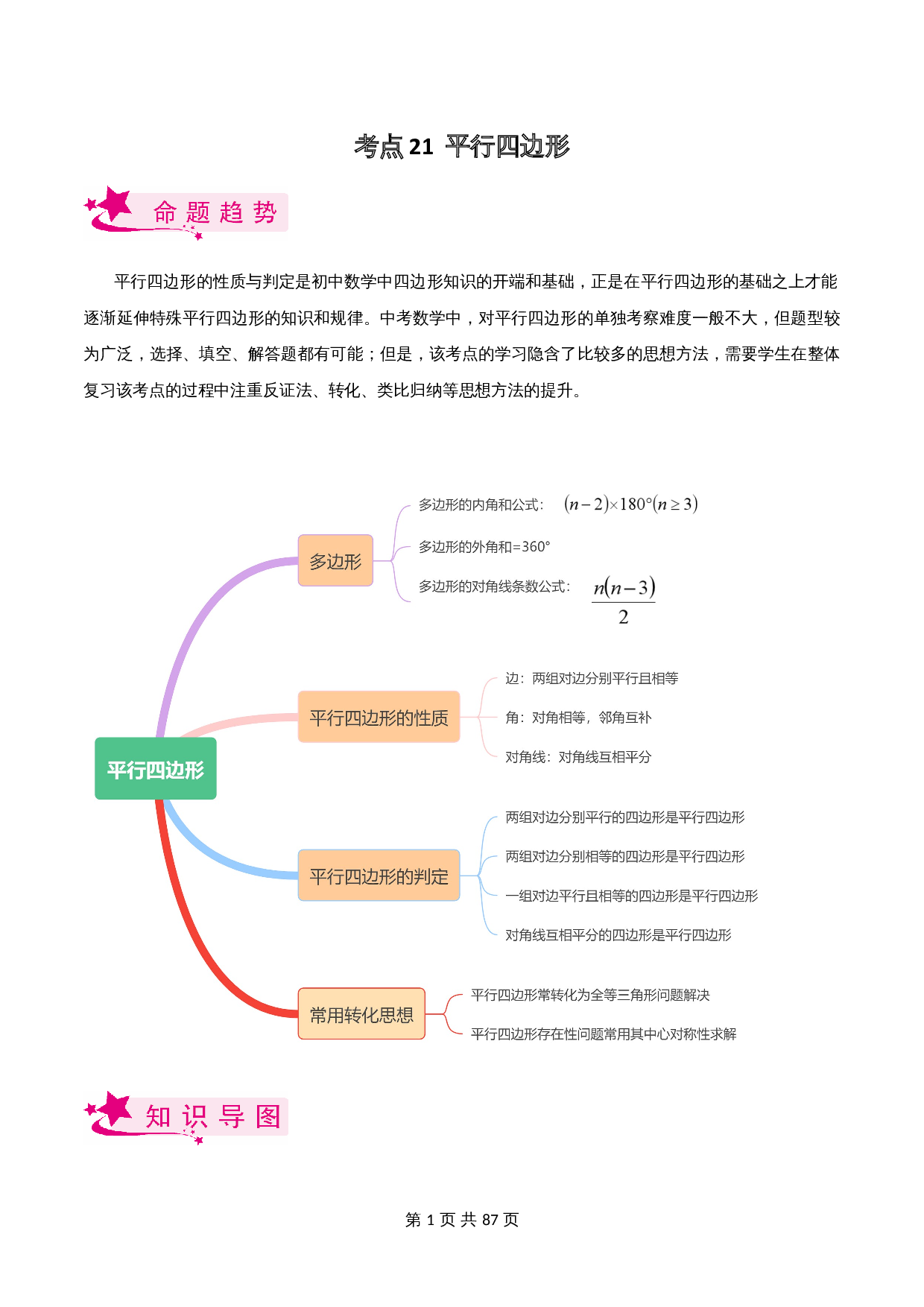
多边形
平行四边形的性质
平行四边形的判定
平行四边形的存在性
考向一:
多边形
多边形与正多边形
正多边形定义
各边都相等,各角都相等的多边形为正多边形
多边形与正多边形的性质
n边形的内角和为
任意多边形的外角和为360
°
任意多边形的内角中,最多有3个锐角
n边形共有
条对角线
正多边形都是轴对称图形,变数为偶数的正多边形还是中心对称图形
1.若一个
n
边形从一个顶点最多能引出6条对角线,则
n
是( )
A.5
B.8
C.9
D.10
2.我们学习多边形后,发现凸多边形的对角线有一定的规律,
①
中的四边形共有2条对角线,
②
中的五边形共有5条对角线,
③
中的六边形共有9条对角线,
…
,请你计算凸十边形对角线的总条数( )
A.54
B.44
C.35
D.27
3.一个多边形的内角和为1080
°
,它为( )边形.
A.10
B.6
C.8
D.12
4.如果一个多边形的内角和等于其外角和的2倍,那么这个多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
考向
二
:
平行四边形的性质
平行四边形的性质定理
∶
平行四边形的对边平行且相等.
平行四边形的对角相等,邻角互补.
平行四边形的对角线互相平分.
利用平行四边形的性质证明边、角关系时,一定要找准那些对解题有帮助的性质,有时也可以根据结论逆向推理看是否符合那些性质.
平行四边形的问题经常转化为三角形全等的判定与性质类问题应用。
1.关于平行四边形的性质,下列描述错误的是( )
A.平行四边形的对角线相等
B.平行四边形的对角相等
C.平行四边形的对角线互相平分
D.平行四边形的对边平行且相等
2.如图,在平行四边形
ABCD
中,
∠
A
﹣∠
B
=50
°
,则
∠
A
的度数是( )
A.130
°
B.115
°
C.65
°
D.50
°
3.在平行四边形
ABCD
中,
∠
A
的角平分线把边
BC
分成长度为4和5的两条线段,则平行四边形
ABCD
的周长为( )
A.13或14
B.26或28
C.13
D.无法确定
4.如图,在
▱
ABCD
中,
BF
平分
∠
ABC
交
AD
于点
F
,
CE
平分
∠
BCD
交
AD
于点
E
,若
AB
=
【考点讲练测】考点21 平行四边形(含解析)-2024年中考数学一轮复习(全国通用)