【几何模型解密】专题05 A字型、8字模型、飞镖模型（含解析）-2024年中考数学一轮复习满分突破（全国通用）

专题05 A字型、 8字 模型、 飞镖模型 一、基础知识回顾 三角形内角和定理： 三角形三个内角和等于180° 三角形外角性质： 三角形的一个外角等于与它不相邻的两个内角之和。 二、 模型的概述： A字型模型： ∠1+∠2=∠ A +1 80 ° （结论） 证明： ∵∠1=∠A + ∠ ACB ∴∠1=∠A + 180°-∠2 ∴∠1+∠2=∠ A +1 80 ° 8字模型（基础）：∠ A +∠ B =∠ C +∠ D （结论） 证明： 在 ∆ABO 中，∠ A +∠ B +∠ AOB =180° 在 ∆COD 中，∠ C +∠ D +∠C OD =180° 而∠ AOB =∠C OD ∴∠ A +∠ B =∠ C +∠ D 8字模型（变形）： 已知线段A P 平分∠ BAD ，线段C P 平分∠ BCD ，则 ∠P= (∠B+∠D) 证明：∵ 线段A P 平分∠ BAD ，线段C P 平分∠ BCD ∴∠B AP= ∠P AD, ∠B CP= ∠P CD ∵∠B CP+ ∠P = ∠B AP+ ∠B ① ∠ PAD+ ∠ P= ∠ PCD+ ∠ D ② ①+②得2∠P=∠B + ∠ D ， 则∠P= (∠B+∠D) 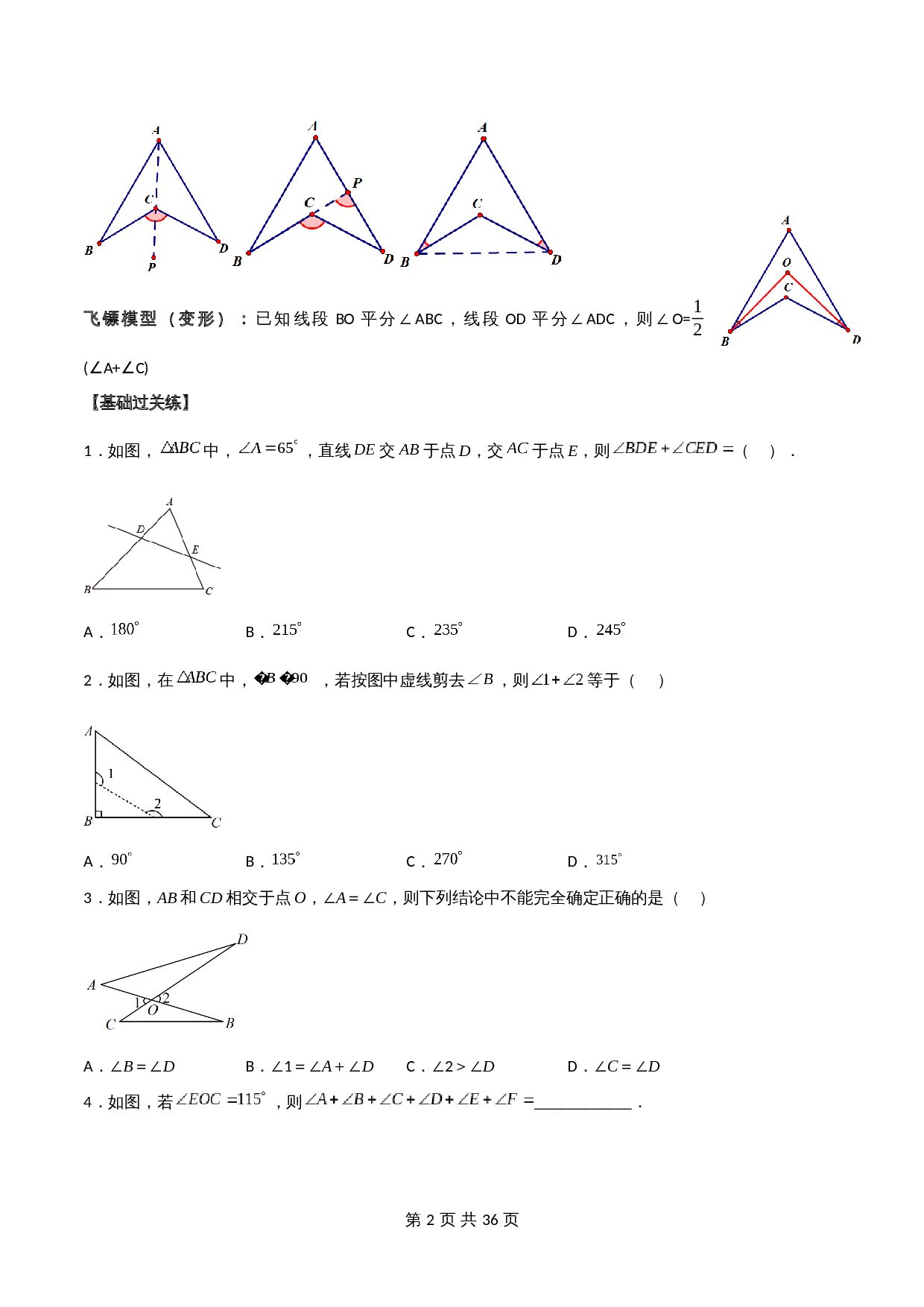飞镖模型（基础）：∠C=∠A+∠B+∠D （结论） 证明： 1）延长A C 到点P 2）延长B C 交A D 于点 P 3）连接B D 飞镖模型（变形）： 已知线段 BO 平分∠A BC ，线段 OD 平分∠ ADC ，则∠O= (∠A+∠C) 【基础过关练】 1．如图， 中， ，直线 交 于点 D ，交 于点 E ，则 （      ）． A． B． C． D． 2．如图，在 中， ，若按图中虚线剪去 ，则 等于（　 ） A． B． C． D． 3．如图， AB 和 CD 相交于点 O ，∠ A ＝∠ C ，则下列结论中不能完全确定正确的是（      ） A．∠ B ＝∠ D B．∠1＝∠ A ＋∠ D C．∠2＞∠ D D．∠ C ＝∠ D 4．如图，若 ，则 ____________． 5．如图所示，已知四边形 ，求证 ． 【提高测试】 1．如图，∠1=60°，则∠A+∠B+∠C+∠D+∠E+∠F=（　　） A．240° B．280° C．360° D．540° 2．如图，在由线段 组成的平面图形中， ，则 的度数为（      ）． A． B． C． D． 3．如图，在 △ ABC 中，∠ A =20°，∠ ABC 与∠ ACB 的角平分线交于 D 1 ，∠ ABD 1 与∠ ACD 1 的角平分线交于点 D 2 ，依此类推，∠ ABD 4 与∠ ACD 4 的角平分线交于点 D 5 ，则∠ BD 5 C 的度数是（　　） A．24° B．25° C．30° D．36° 4．如图，求∠ A +∠ B +∠ C +∠ D +∠ E +∠ F +∠ G +∠ H +∠ I ＝__． 5．如图， ____________． 6．如图， 平分 ，交 于点 F ， 平分 交 于点 E ， 与 相交于点 G ， ． （1）若 ，求 的度数； （2）若 ，求 的度数． 7．（1）已知：如图①的图形我们把它称为“ 字形”，试说明： ． （2）如图②， ， 分别平分 ， ，若 ， ，求 的度数． （3