【压轴题】专题3二次函数与等腰直角三角形问题（全国通用）（含解析）-2024年中考数学复习

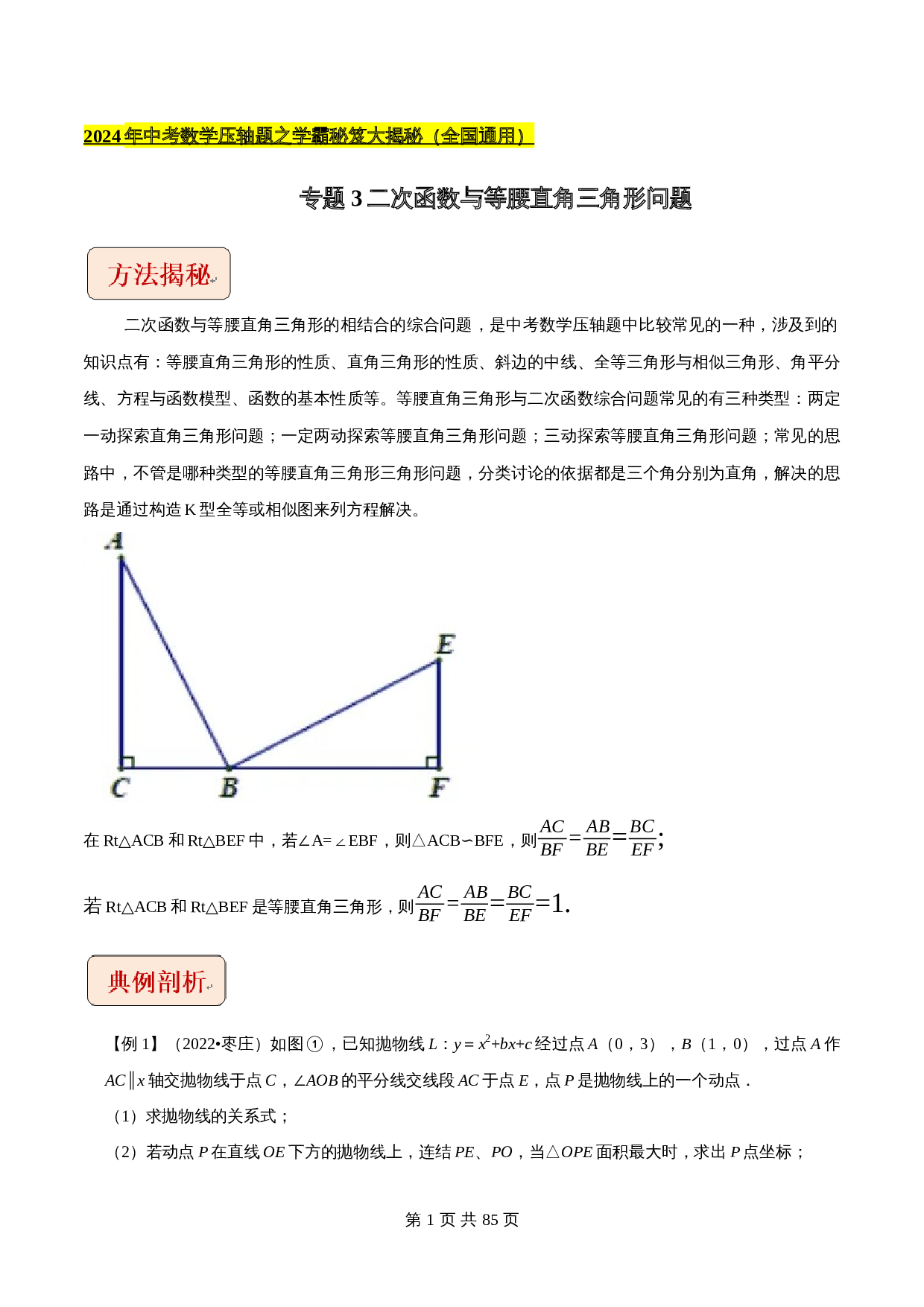
2024年中考数学压轴题之学霸秘笈大揭秘（全国通用） 专题3二次函数与等腰直角三角形问题 二次函数与等腰直角三角形的相结合的综合问题，是中考数学压轴题中比较常见的一种，涉及到的知识点有：等腰直角三角形的性质、直角三角形的性质、斜边的中线、全等三角形与相似三角形、角平分线、方程与函数模型、函数的基本性质等。等腰直角三角形与二次函数综合问题常见的有三种类型：两定一动探索直角三角形问题；一定两动探索等腰直角三角形问题；三动探索等腰直角三角形问题；常见的思路中，不管是哪种类型的等腰直角三角形三角形问题，分类讨论的依据都是三个角分别为直角，解决的思路是通过构造K型全等或相似图来列方程解决。 在Rt△ACB和Rt△BEF中，若∠A=∠EBF，则△ACB∽BFE，则 = ; 若 Rt△ACB和Rt△BEF是等腰直角三角形，则 = =1. 【 例1 】 （2022•枣庄）如图 ① ，已知抛物线 L ： y ＝ x 2 + bx + c 经过点 A （0，3）， B （1，0），过点 A 作 AC ∥ x 轴交抛物线于点 C ，∠ AOB 的平分线交线段 AC 于点 E ，点 P 是抛物线上的一个动点． （1）求抛物线的关系式； （2）若动点 P 在直线 OE 下方的抛物线上，连结 PE 、 PO ，当△ OPE 面积最大时，求出 P 点坐标； （3）将抛物线 L 向上平移 h 个单位长度，使平移后所得抛物线的顶点落在△ OAE 内（包括△ OAE 的边界），求 h 的取值范围； （4）如图 ② ， F 是抛物线的对称轴 l 上的一点，在抛物线上是否存在点 P ，使△ POF 成为以点 P 为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点 P 的坐标；若不存在，请说明理由． 【 例2 】 （2022•东营）如图，抛物线 y ＝ ax 2 + bx ﹣3（ a ≠0）与 x 轴交于点 A （﹣1，0），点 B （3，0），与 y 轴交于点 C ． （1）求抛物线的表达式； （2）在对称轴上找一点 Q ，使△ ACQ 的周长最小，求点 Q 的坐标； （3）点 P 是抛物线对称轴上的一点，点 M 是对称轴左侧抛物线上的一点，当△ PMB 是以 PB 为腰的等腰直角三角形时，请直接写出所有点 M 的坐标． 【 例3 】 （2022•吉林）如图，在平面直角坐标系中，抛物线 y ＝ x 2 + bx + c （ b ， c 是常数）经过点 A （1，0），点 B （0，3）．点 P 在此抛物线上，其横坐标为 m ． （1）求此抛物线的解析式． （2）当点 P 在 x 轴上方时，结合图象，直接写出 m 的取值范围． （3）若此抛物线在点 P 左侧部分（包括点 P ）的最低点的纵坐标为2﹣ m ． ① 求 m 的值． ② 以 PA 为边作等腰